| Written on the Wall II is composed mainly of conjectures
of my conjecture-making program Graffiti.pc (G.pc for short)
which was inspired by Siemion Fajtlowicz's conjecture-making program
Graffiti. Both programs utilize Fajtlowicz's Dalmatian
heuristic, however each has its individual implementations. The first 8
conjectures were generated by Graffiti, while I was Fajtlowicz's student,
see
1996 list(pdf)
for the original list. The remaining conjectures on this list (as of 2001) were generated by Graffiti.pc. Please send information to
delavinae@uhd.edu on any of the conjectures on this list. Related
websites and papers
Siemion
Fajtlowicz's list (with comments)
Written on the Wall is available from him by request. Also available is
bibliographical information on papers inspired by conjectures of
Graffiti, since it inception in the mid-1980s; that webpage includes a
variety of papers related to Graffiti.
Some of the most recent papers that describe and discuss Graffiti include:
| |
E. DeLaVina, On Some History of the Development of Graffiti
(ps)
(pdf),
Graphs and Discovery DIMACS: Series in Discrete Mathematics and
Theoretical Computer Science, 69(2005), 81-118. S. Fajtlowicz, Toward Fully Automated Fragments of Graph Theory II,
(pdf).
C. E. Larson, A Survey in Automated Mathematical
Conjecture-Making
(pdf),
Graphs and Discovery DIMACS: Series in Discrete Mathematics and
Theoretical Computer Science, 69(2005), 297-318..
|
Papers describing Graffiti.pc include:
| |
section 5 of the above paper "On Some History of the
Development of Graffiti" and
|
| |
E. DeLaVina, Graffiti.pc: A Variant of Graffiti,
(pdf),
Graphs and Discovery DIMACS: Series in Discrete Mathematics and
Theoretical Computer Science, 69(2005), 71-79.
|
|
|
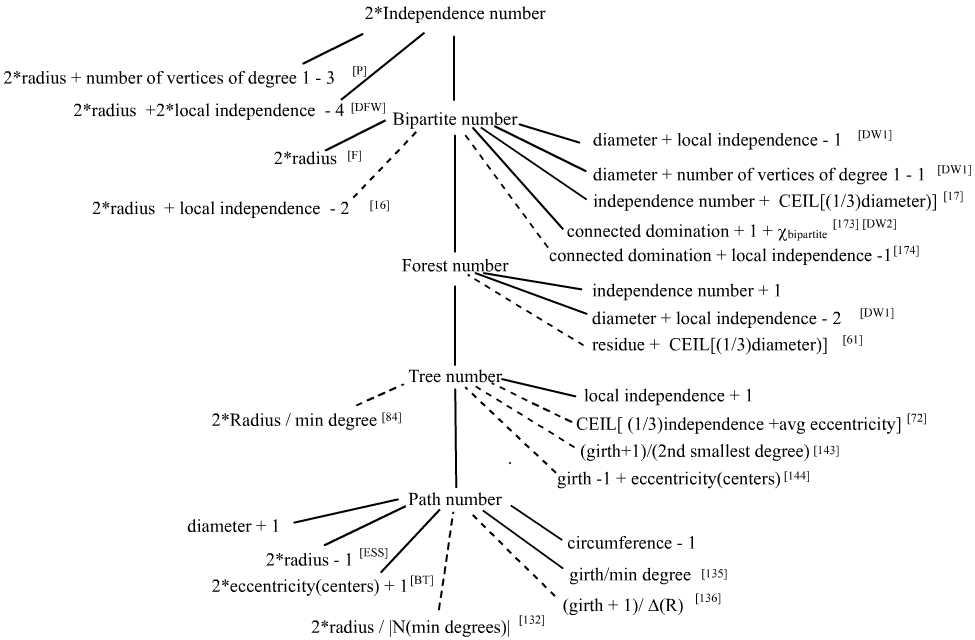
| At the moment, a majority of conjectures on
Written on Wall II are lower bounds on the maximum order of certain
induced subgraphs of a connected graph. The
bipartite number of a graph is the order of a largest induced
bipartite subgraph of the graph; the forest, tree and
path numbers are the orders of largest induced forests, trees and
paths, resp., of a graphs.
The diagram below (you may have to scroll down) illustrates the relationship between (by means
of a solid line) the bipartite, forest, tree and path numbers, namely that
bipartite number ≥ forest number ≥ tree number ≥ path number.
The
diagram presents other correct relations also through solid lines using the
convention that a line emanating from an invariant down to an expression
of invariants represents the relation greater than or equal to. For
instance, it is known that for a simple connected graph, the path number ≥
2*radius - 1 (a result of F. Chung in [ESS]). On the other hand, a dashed
line indicate a conjectured relation between the expressions. For
instance, G.pc's conjecture #17 is that for a simple connected
graph, the bipartite number ≥ independence number + CEIL[(1/3)diameter]
(to see all open conjectures of G.pc click on the menu on the left). Relations that are not referenced with a paper or conjecture number are
simple exercises, such as bipartite number ≥ forest number ≥ tree number ≥
path number ≥ diameter + 1; such relations are listed in order to emphasize
that many of G.pc's conjectures on maximum induced subgraphs propose
improvements on these simple propositions.
References
| [BT] |
G. Bacso and Z. Tuza, A characterization
of graphs without long induced paths, Journal of Graph Theory,
14(1990), 455-464. |
| [DFW] |
E. DeLaVina, S. Fajtlowicz and B. Waller,
On Some conjectures of Griggs and Graffiti, Graphs and Discovery
DIMACS: Series in Discrete Mathematics and Theoretical Computer
Science, 69(2005), 119-125. |
| [DW1] |
E. DeLaVina and B. Waller,
On some conjectures of graffiti.pc on the maximum order of induced
subgraphs (pdf), Congressus Numerantium, 2004 |
| [DW2] |
E. DeLaVina and B. Waller,
Spanning trees with many leaves and the maximum order of bipartite
Subgraphs, 2005 (preprint) |
| [ESS] |
P. Erdos,, M. Saks, and V. Sos, Maximum
induced trees in graphs, Journal of Graph Theory, 41(1986), p. 61-79.
|
| [F] |
S. Fajtlowicz, A characterization of
radius-critical graphs, Journal of Graph Theory, 12(1988), p. 529-532. |
| [P] |
R. Pepper, ...., Preprint |
|
|