A relation on the set A is a relation from A to A.
Recall: A binary relation R from A
to B is a subset of the Cartesian product ![]() If
If ![]() , we
write xRy and say that x is related to y with respect
to R.
, we
write xRy and say that x is related to y with respect
to R.
A relation on the set A is a relation from A to A.
Examples: Given the following relations on Z,
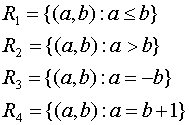
a. For which relations is it the case that "2
is related to -2"?
b. For which relation is it the case that (0,1) belongs
to the relation?
Exercise: How many relations are there on a set with n-elements?
Ans: By definition a relation is a subset
of the Cartesian product A X A. So the question translates into how many
subsets are there of the Cartesian product A X A? By known result the answer
is![]() .
.
Properties of Relations:
Definition: A relation R on a set A is called reflexive if aRa for every element a in A.
A relation R on a set A is called symmetric if aRb whenever bRa.
A relation R on a set A is called transitive
if whenever aRb and bRc, then aRc, for a, b
and c in A.
Exercises: Which of the following relations are reflexive, symmetric and /or transitive.
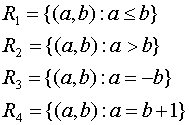
R5 = {(x,y) : x and y have the same father}
R6 = {(x,y) : x is the mother of y}
![]()
Combining relations:
Example: Let A = {1,2, 3} and B = {1, 2,3, 4}. Given the relations R1={ (1,1), (2,2), (3,3)} and R2={(1,1),(1,2), (1,3), (1,4)}, find
![]() =
{
(1,1), (2,2,), (3,3), (1,2), (1,3), (1,4) }
=
{
(1,1), (2,2,), (3,3), (1,2), (1,3), (1,4) }
![]() =
{
(1,1)}
=
{
(1,1)}
![]() =
{
(2,2,), (3,3) }
=
{
(2,2,), (3,3) }
![]() =
{
(1,2), (1,3), (1,4) }
=
{
(1,2), (1,3), (1,4) }
Definition: Let R be a relation from a set A
to a set B and S a relation from B to a set C.
The composite of R and S is the relation consisting of ordered
pairs (a,c), where a is from A and c is in
C,
and for which there exists an element b in B such that aRb
and
bSc. We denote the composite of R and
S by![]()
Example: Suppose R is a relation from A to B
and S is a relation from B to C , where A= {1, 2,3}, B = { 1, 2,3, 4},
and C = {0, 1,2} with R = { (1, 1), (1,4), (2, 3), (3, 1), (3, 4)} and
S = { (1,0), (2,0), (3,1), (3,2), (4,1)}. What is the composite relation
of R and S?
![]()
Convenient Representation for binary relations on a
set:
Let A be an n-element set, B be an m-element
set, and ![]() .
A convenient representation for R is as an
.
A convenient representation for R is as an ![]() matrix
[rij] in which
matrix
[rij] in which
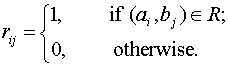
Note that this is a characteristic function on ![]() for the relation R.
for the relation R.
Queries:
Theorem(composite relations) Let ![]() and
and ![]() be
relations. Then the matrix of the relation
be
relations. Then the matrix of the relation ![]() is
equal to the product of the matrices for relations R and S.
is
equal to the product of the matrices for relations R and S.
Equivalence Relations
Definition: A relation on a set A is called an equivalence
relation if it is reflexive , symmetric and transitive.
Example: Let R be the relation on the set of
real numbers such that a R b if and only if a - b is an integer. Is R an
equivalence
relation?
Example: Let m be a positive integer greater
than 1. Show that the relation R = { (a,b) : ![]() is an equivalence relation.
is an equivalence relation.
Equivalence Classes:
Let R be an equivalence relation on a set A. The set of all elements that are related to an element a of A is called the equivalence class of a. The notation is [a]R.
Example: Given the equivalence relation R =
{ (a,b) : ![]() , list the elements
of
, list the elements
of
[0] =
[1] =
[2] =
[4] =
Theorem. Let R be an equivalence relation on a set A. The following statements are equivalent:
Example: Given the set A = {1, 2, 3, 4, 5, 6}.
Describe an equivalence relation that produces the following equivalence
classes {1,3} , { 2, 4}, and {5, 6}.
Definition: A partition of a set A is
a collection of disjoint nonempty subsets of A such that their union is
the set A.
Theorem: Let R be an equivalence relation on
a set A. Then the equivalence classes of R form a partition of S. Conversely,
given a partition {Ai : i is in I} of the set A, there is an
equivalence relation R that has the sets Ai, i in I as its equivalence
classes.
More Homework:
(a) 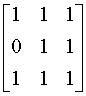 (b)
(b) 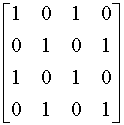 (c)
(c)