13.2 VECTORS

Vectors from a Geometric Viewpoint

A vector is a quantity that has both magnitude and direction.

A vector is often represented by an arrow or a directed line segment:

- the length of the arrow represents the magnitude of the vectorl and

- the arrow points in the direction of the vector.

In Figure 1:

The vector v has initial point A (the tail) and terminal point B (the tip).

We write

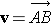
Note that vector u has the same length and direction as vector v but it is in a different position.

We say u and v are equivalent (or equal) and write

u = v

Hence, a given vector may be positioned anywhere in the plane as long as the length and direction of the vector remain unchanged.

 

The zero vector, denoted by 0, has length 0. It is the only vector with no specific direction.

 

Arithmetic of Vectors

To add vectors, we position the vectors so that the terminal point of one coincides with the initial point of the other.

 

Definition of Vector Addition - Triangle Law

If u and v are vectors positioned so the initial point of v is at the terminal point of u, then the sum

u + v

is the vector from the initial point of u to the terminal point of v.

The definition of vector addition is illustrated in Figure 3 - this definition is sometimes called the Triangle Law.

 

Definition of Vector Addition - Parallelogram Law

It is also possible to construct the sum u + v by positioning u and v so the initial points coincide.

Then we complete the parallelogram as shown in Figure 4. The sum lies along the diagonal of the parallelogram with u and v as sides.

 

Figure 4 also illustrates that vector addition is a commutative operation.

u + v = v + u

 

Note:

It is possible to change the length of a vector, that is to "scale" a vector, by multiplying the vector by a real number.

A real number is called a scalar to distinguish it from a vector.

 

Definition of Scalar Multiplication

If c is a scalar and v is a vector, then the scalar multiple cv is the vector

whose length is |c| times the length of v and

whose direction is the same as v if c > 0 and is opposite to v if c < 0.

If c = 0 or v=0, then cv = 0.

 

This defintion is illustrated in Fiture 7.

 

Note:

Two nonzero vectors are parallel if and only if they are scalar multiples of one another.

 

The Negative of a Vector and the Difference of Two Vectors

The vector

-v = (-1)v

has the same length as v but points in the opposite direction. See Figure 7.

This vector is called the negative of v.

 

By the difference u - v we mean

 

u - v = u + (-v)

 

In Figure 8a, we use the Parallelogram Law since u - v = u + (-v).

In Figure 8b, we use the Triangle Law since v + (u - v) = u.

 

Vectors from an Algebraic Viewpoint

For some purposes, it is best to introduce a coordinate system and treat vectors algebraically.

If we place the initial point of a vector a at the origin of a rectangular coordinate system, then the terminal point of a has coordinates of the form (a₁, a₂) or (a₁, a₂, a₃) depending on whether the coordinate system is two- or three-dimensional. These coordinates are called the components of a and we write

a = <a₁, a₂> or a = <a₁, a₂, a₃>.

Note the vector

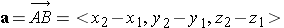
has initial point at the origin and terminal point (3, 2).

All vectors that are equal or equivalent to the vector a are representations of the algebraic vector a = <3, 2>.

 

For each of these vectors, the terminal point can be reached from the initial point by a displacement of three units to the right and two upward.

That is if

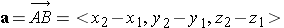
then

a₁ + 3 = b₁ and a_{2 + 2} = b₂

Note also that

 

3 = b₁ - a₁ and 2 = b₂ - b₁

 

The particular representation from the origin to the point (3, 2) is called the position vector of the point P.

 

In three dimensions the vector

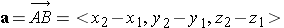
is the position vector of the point (a₁, a₂, a₃).

 

In general:

 

Given the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂), the vector a with representation AB is

 

 

Magnitude of a Vector

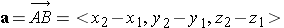
The magnitude or length of a vector v is the length of any of its representations and is denoted by | v |.

In particular, if we use the position vector with initial point the origin, we can use the distance formula to find the following formulas.

 

The length of a two dimensional vector

The length of the vector a = <a₁, a₂> is

 

 

The length of a three dimensional vector

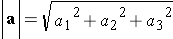
The length of the vector a = <a₁, a₂, a₃> is

 

 

 

 

 

Operating on Vectors Algebraically

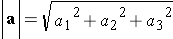
If a = <a₁, a₂> and b = <b₁, b₂>, then

(1) a + b = <a₁ + b₁, a₂ + b₂>

 

(2) a - b = <a₁ - b₁, a₂ - b₂>

 

(3) ca = <ca₁, ca₂>

 

Similarly for three-dimensional vectors.

 

 

 

 

 

 

toc | return to top