13.1 Three-Dimensional Coordinate Systems
In a plane, we use two coordinate axes, the x-axis and y-axis, that are perpendicular to each other to determine the location of any point in the plane.
A point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
Hence, a plane is called two-dimensional.
In space, we use three coordinate axes, the x-axis, y-axis and z-axis, (each of which is perpendicular to the other two) that meet at a point O, the origin.
A point in space can be represented as an ordered triple (a, b, c) of real numbers, where a is the x-coordinate, b is the y-coordinate and c is the z-coordinate.
Hence, space is called three-dimensional.
To locate a point P(a, b, c), we can start at the origin O, move a units along the x-axis, then b units parallel to the y-axis, and then c units parallel to the z-axis.
The three coordinate axes determine the three coordinate planes.
The xy-plane is the plane that contains the x- and y-axes;
the yz-plane is the plane that contains the y- and z-axes;
the xz-plane is the plane that contains the x- and z-axes.
If P(x, y, z) is a point in space, then
x is the directed distance from the yz-plane to the point P,
y is the directed distance from the xz-plane to the point P, and
z is the directed distance from the xy-plane to the point P.
For the point P(3, 2, 6), determine the directed distance from each coordinate plane.

The Cartesian product RxR is the set of all ordered pairs of real numbers and is denoted by R2.
RxR = { (x, y) | x, y ε R }
The Cartesian product RxRxR is the set of all ordered triples of real numbers and is denoted by R3.
RxRxR = { (x, y, z) | x, y, z ε R }
There is a one-to-one correspondence between the points in space and the ordered triples in R3.
It is called a three-dimensional rectangular coordinate system.
The three coordinate axes divide space into eight regions called octants, and the first octant is the set of points whose coordinates are all positive.
In two-dimensional analytic geometry, the graph of an equation in the variables x and y is a curve in R2.
In three-dimensional analytic geometry, the graph of an equation in the variables x, y and z is a surface in R3.
Describe the surface in R3 represented by each equation.
(a) z = 3 (b) y = 5
Solution
(a). In R3 , the equation z = 3 represents the set of all points
{ (x, y, z) | x, y ε R, z = 3 }
This set contains infinitely many points.
However, each point (x, y, 3) in this set has a common property: each point lies 3 units above the xy-plane.
That is, this set of points is the horizontal plane that is parallel to the xy-plane and is 3 units above it.
(b) Similarly, in R3 , the equation y = 5 represents the set of all points
{ (x, y, z) | x, z ε R, y = 5 }
Each point (x, 5, z) in this set lies 5 units above the xz-plane.
So this set of points is the vertical plane that is parallel to the xz-plane and is 5 units to its right.
Let k be a constant (a real number). Then
(1) The graph of the equation x = k in R3 is a plane parallel to the yz-plane;
(2) The graph of the equation y = k in R3 is a plane parallel to the xz-plane;
(3) The graph of the equation z = k in R3 is a plane parallel to the xy-plane;
YOU TRY IT
Describe the region of R3 that is represented by the inequality y > 5.
The formula for the distance between two points in the plane can be extended to two points in space.
Distance Formula in Three Dimensions
The distance | P1P2 | between the points P1(x1, y1, z1) and P2(x2, y2, z2) equals
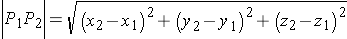
Study the figure below: can you explain how to derive this formula? (Hint: use the Pythagorean theorem twice.)
(a) Find the distance between the points P(2, -1, 7) and Q(3, 1, 5).

(b) Find the equation of a sphere with radius r and center C(h, k, l).

Given three points in space, how are the distances between them related if the points lie on a straight line?

Section 13.1 - Suggested Exercises
# 1, 3, 7, 9, 11, 13, 15, 17, 21, 23, 25, 29, 33, 35